4.19. Información de Superficie

En Topografía se entiende por superficie natural aquella superficie cuya forma es coincidente con la de la realidad física que se pretende caracterizar. Sin embargo, la naturaleza propia de los sistemas de representación gráfica, así ocurre entre otros en el sistema de planos acotados, obliga a adoptar su proyección ortogonal sobre un plano de referencia horizontal como la superficie representada, asignándole la denominación de superficie topográfica, agraria o reducida (ver figura). La superficie topográfica es siempre menor o igual a la superficie natural ya que la primera de ellas es plana mientras ésta última es generalmente curva. Por otro lado hay que tener en cuenta que dos superficies reales distintas pueden corresponder a una misma superficie horizontal. Generalmente es la superficie topográfica la que tiene interés —es la que se representa en planos y mapas—, aunque pueden presentarse circunstancias en las que la superficie natural sea el mensurando objetivo, como por ejemplo, en casos en que se pretendan cuantificar tratamientos superficiales. Ambas superficies han de ser, por tanto, consideradas.

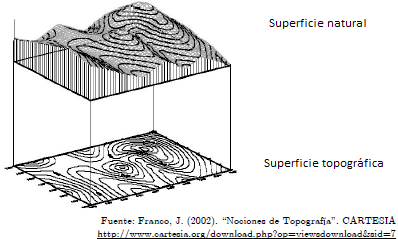
La representación del terreno no puede suponer la proyección de todos sus puntos, por lo que se recurre a proyectar únicamente algunos puntos característicos que permiten determinar su forma y dimensiones. Estos puntos pueden ser constitutivos de una curva de nivel —curvas obtenidas por la proyección de puntos de una determinada altitud o cota— o bien puntos aislados característicos.

La ejecución del presente comando devuelve una ventana informativa en la que se indican los datos básicos de la superficie. Dicha ventana recoge, primeramente, la denominación de la superficie, el número de vértices y el de triángulos que constituyen la malla correspondiente a dicha superficie, los perímetros de la malla (perímetro 3D) y de su proyección horizontal (perímetro 2D) y las áreas tanto de su superficie natural (3D) como de la topográfica (2D). Adicionalmente se muestran las cotas máxima y mínima de dicha superficie.

En el caso de que los puntos que se usaron al crear la superficie tuviesen datos de incertidumbres, pulsando el botón Calcular Incertidumbres se ejecutará el proceso de cálculo y tras su finalización aparecerá un nuevo diálogo en el que se mostrarán todos los datos con sus incertidumbres correspondientes.

Debe tenerse en cuenta que el nivel de confianza para el cálculo de la incertidumbre (por defecto 95 %) se establece en la configuración de Topografía. Ver el Manual de Personalización para más detalles.

En el caso del cálculo de la superficie topográfica (2D) mediante la fórmula de Gauss, el método consiste en:

1. Determinar las coordenadas de posición de cada punto objetivo —nube de puntos— a partir de las observaciones taquimétricas correspondientes o bien, cuando las observaciones sean satelitales (GNSS), disponer de dichas coordenadas por haber sido éstas calculadas previamente por los sistemas GNSS implicados en cada trabajo.

2. Generar, con o sin constricciones debidas a la predeterminación de puntos de perímetro, líneas de rotura —líneas de cambios bruscos y localizados de pendiente— y/o otros puntos característicos; la malla triangular asociada a cada trabajo. Esta tarea supondrá asignar a cada triángulo tres puntos de la nube, de coordenadas conocidas, así como determinar los puntos que son considerados perimetrales, que son los únicos que serán tenidos en cuenta para el cálculo

posterior.

3. Aplicar la fórmula de Gauss que relaciona la superficie plana de un polígono con las coordenadas de posición de sus vértices sucesivos, cuyo resultado será la superficie topográfica (2D).

El cálculo de superficies naturales (3D) por el método de Herón consiste en:

1. Determinar las coordenadas de posición de cada punto objetivo —nube de puntos— a partir de las observaciones taquimétricas correspondientes o bien, cuando las observaciones sean satelitales (GNSS), disponer de dichas coordenadas por haber sido éstas calculadas previamente por los sistemas GNSS implicados en cada trabajo.

2. Generar, con o sin constricciones debidas a la predeterminación de puntos de perímetro, líneas de rotura —líneas de cambios bruscos y localizados de pendiente— y/o otros puntos característicos; la malla triangular asociada a cada trabajo. Esta tarea supondrá asignar a cada triángulo tres puntos de la nube de coordenadas conocidas.

3. Calcular las longitudes de los lados de cada triángulo constitutivo de la malla considerando bien sus coordenadas tridimensionales, si el cálculo que se pretende es el de superficies naturales (3D); o bien sus coordenadas planas, si el cálculo que se pretende es el de la superficie topográfica (2D). En ambos casos este cálculo se basará en el del módulo de un vector determinado por dos puntos.

4. Determinar el área de cada triángulo por aplicación de la fórmula de Herón que relaciona la superficie de un triá ngulo plano con la longitud de cada uno de sus lados.

5. Sumar las superficies de cada uno de los triángulos constitutivos de la malla triangular asociada a un trabajo concreto cuyo resultado será finalmente la superficie natural (3D), si el cálculo de la longitud de cada lado de cada triángulo se hizo considerando sus coordenadas tridimensionales; o la superficie topográfica (2D), si el cálculo se hizo considerando únicamente sus coordenadas

planas.

Finalmente a cada uno de estos modelos matemáticos de cálculo de superficies se les aplican las leyes de propagación de varianzas y covarianzas para determinar las incertidumbres de la superficie topográfica (2D) o natural (3D).