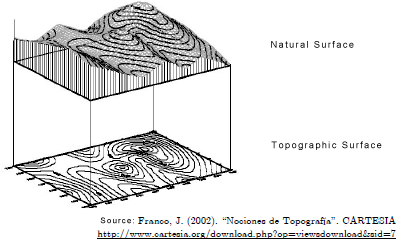
In Topography natural surface means the surface the shape of which coincides with the physical reality we intend to represent. However, the very nature of the graphic representation systems, as occurs in the bounded plane system, among others, obliges us to use its orthogonal projection on a horizontal reference plane as the most common surface, assigning it the name topographic, agrarian or reduced surface (see the figure). The topographic surface is always smaller or equal to the natural surface as the former is flat and the latter may be curved. Moreover, we need to consider that two real different surfaces may correspond to the same horizontal surface. It is normally the topographic surface we are interested in – that represented in plans and maps -, although circumstances may exist where the natural surface is the target measurand, such as, for example, in cases of quantifying surface treatment. Therefore, both surfaces need to be considered.
The representation of the terrain cannot entail the projection of all its points, and as such features only a number of characteristic points which enable us to determine the shape and dimensions of the same. These points may comprise a contour — obtained by projecting the points of a given altitude or height — or characteristic isolated points.
The execution of this command opens an informative window in which we specify the basic surface data. This window provides, first and foremost, the name of the surface, the number of vertices and triangles comprising the grid pertaining to the surface in question, the grid perimeters (3D perimeter), the horizontal projection of the same (2D perimeter) and the areas both of its natural (3D) and topographic surface (2D). Moreover, the maximum and minimum heights of the surface in question are also displayed.
In the event the points used when creating the surface contained data on uncertainties, clicking on the Calculate Uncertainty button will execute the calculation process and once it has been concluded a new dialog box will appear featuring all the data and the corresponding uncertainties.
It should be considered that the confidence level for calculating uncertainty (by default, 95%) is established in the Surveying settings. See the Customization Manual for further details.
In the event the calculation of the topographic surface (2D) is conducted using the Gauss formula, the method consists of:
1. Determining the position coordinates of each target point — points cloud — based on the corresponding tachymetric observations or, when the observations are conducted by satellite (GNSS), having such coordinates at hand, as these are the coordinates which have been calculated beforehand by the GNSS systems involved in each task.
2. Generating, with or without restrictions due to the predetermination of perimeter points, break lines — lines with sudden changes in slope — and/or other characteristic points; the triangular grid associated with each assignment. This task will involve assigning to each triangle three points from the cloud of known coordinates, as well as determining the points regarded as perimetral, which are the only ones to be considered for the subsequent calculation.
3. Applying the Gauss formula which associates the flat surface of a polygon with the position coordinates of its successive vertices, the result of which will be the topographic surface (2D).
The calculation of natural surfaces (3D) using Heron’s method consists of:
1. Determining the position coordinates of each target point — points cloud — based on the corresponding tachymetric observations or, when the observations are conducted by satellite (GNSS), having such coordinates at hand, as these are the coordinates which have been calculated beforehand by the GNSS systems involved in each task.
2. Generating, with or without restrictions due to the predetermination of perimeter points, break lines — lines with sudden changes in slope — and/or other characteristic points; the triangular grid associated with each assignment. This task will involve assigning to each triangle three points from the cloud of known coordinates.
3. Calculating the lengths of the sides of each triangle comprising the grid, considering its three-dimensional coordinates if the desired calculation is for natural surfaces (3D); or its flat coordinates if the desired calculation is for topographic surfaces (2D). In both cases this calculation will be based on that of the module of a vector specified by two points.
4. Determining the area of each triangle using Heron’s formula, which associates the surface of a flat triangle with the length of each of its sides.
5. Adding up the surfaces of each of the triangles comprising the triangular grid associated with a specific task, the final result of which will be the natural surface (3D) if the calculation of the length of each side of each triangle has been conducted using its three-dimensional coordinates; or the topographic surface (2D) if the calculation was conducted using its flat coordinates only.
Finally, each of these mathematical models for the calculation of surfaces is subject to the laws of the propagation of variances and covariances to determine the uncertainties of the topographic (2D) or natural surface (3D).