Angle measurement uncertainty
ISO Standard 17123-3 sets out the procedure to be followed by a user to determine and evaluate the angle measurement uncertainty of the instrument used. Although the quality of the instrument measurement depends on various factors such as offset uncertainty, the angle resolution of the instrument, telescope magnification etc., ISO Standard 17123-3 does to set out to study each of these factors, but rather to ascertain the final effect produced by them all, evaluation the typical deviation of the measurement.
The expression of the combined typical uncertainty of an angle can be evaluated as:
where:
Angle measurement contribution of the station
Pursuant to ISO standard 17123-3, the typical horizontal and vertical angle measurement uncertainty with a theodolite is expressed by means of the typical experimental deviation of the mean of a horizontal angle direction (σISO-HZ) and of the mean of a vertical angle (σISO-V). Hence, for a given angle direction the typical deviation of the measurement encompassing the traditional “accidental reading and aiming errors” will be:
The measurement contribution of horizontal angles will be used in the event of typical experimental deviation of the mean of a horizontal angle direction. In the same way as for vertical angles.
Contribution through stake centering
One of the sources of uncertainty in an angular or distance measurement occurs when the target sign is not perfectly centered. Its contribution to the uncertainty of the horizontal angle is:
where:
D = Distance measured.
ρ = Hundredths of seconds which have a radian: An approximation of this value is: 636619,772.
where:
Uo = a value of 0.75 mm has been assumed as this is the most appropriate value for current stations with optical or laser plummet.
It is divided by 3.5 to achieve a coverage probability of 99.7%
Contribution through instrument centering
One of the sources of uncertainty in an angular or distance measurement occurs when the total station is not perfectly centered at the station point. Its contribution to the uncertainty of the horizontal angle is:
where:
D = Distance measured.
ρ = Hundredths of seconds which have a radian: An approximation of this value is: 636619,772.
where:
Uc = a value of 0.75 mm has been assumed as this is the most appropriate value for current stations with optical or laser plummet.
It is divided by 3.5 to achieve a coverage probability of 99.7%
Contribution through stake inclination
One of the sources of uncertainty when a total station is observed directly at the centre of the prism, when measuring a horizontal angle or the geometric distance, is its lack of verticality compared with the point on which it has stopped. Its contribution to the uncertainty of the horizontal angle is:
where:
m = Prism height.
β = Inclination angle of the target sign on the vertical; for its simplification, the value of 3' has been assumed as the most likely maximum inclination we are going to have. This would correspond to the position where the bubble would be at a tangent to the circumference drawn:
It is divided by 3.5 to achieve a coverage probability of 99.7%
where:
D = Distance measured.
ρ = Hundredths of seconds which have a radian: An approximation of this value is: 636619,772.
Contribution through compensator accuracy
where:
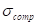= Compensator accuracy in hundredths of seconds.
TcpMDT
