En este apartado se pueden crear sistemas de calibración que permiten transformar las coordenadas proyectadas en coordenadas de un sistema local propio.
Posteriormente se pueden seleccionar en el proyecto activo para trabajar en el sistema local definido.
Basada en los métodos tradicionales de transformaciones de coordenadas y a atendiendo a su dimensión, se ha realizado una clasificación que incluye dichos métodos además de una combinación de algunos de ellos.
Se presentan 3 grupos de transformaciones:
2D : Incluye la transformación de Helmert de 4 parámetros y una traslación de coordenadas en x e y.
Traslaciones 2D
Calcula los desplazamientos x e y mediante la media de la diferencias entre origen y destino. Sólo es necesario un par de puntos.
Fórmulas:
donde:
x', y' = Coordenadas x,y transformadas
x,y = Coordenadas x,y originales
Tx = Traslación x
Ty = Traslación y
Helmert 2D
Es conocida también como transformación de semejanza de 4 parámetros. El proceso de transformación incluye 3 pasos: escalado, rotación y traslaciones.
Los dos primeros están definidos por un parámetro cada uno y las traslaciones incluyen 2. Son necesarios al menos dos pares de puntos.
Fórmulas:
donde:
x', y' = Coordenadas x,y transformadas
x,y = Coordenadas x,y originales
S = Escala
 = Angulo de rotación
= Angulo de rotaciónTx = Traslación x
Ty = Traslación y
3D : Este grupo está formado por la transformación de Helmert de 7 parámetros y una traslación de coordenadas en x, y, z.
Traslaciones 3D
Este tipo de transformación calcula los desplazamientos x, y, z mediante la media de las diferencias entre origen y destino. Sólo es necesario un par de puntos.
Fórmulas:
donde:
x', y’, z' = Coordenadas x,y,z transformadas
x, y, z = Coordenadas x,y,z originales
Tx = Traslación x
Ty = Traslación y
Tz = Traslación z
Helmert 3D
También es conocida como transformación de 7 parámetros. Los parámetros implicados son: tres rotaciones, tres traslaciones y un factor de escala. La matriz de rotación se construye mediante tres giros consecutivos alrededor de los ejes x, y, z. Es necesario disponer al menos de 3 pares de puntos.
Fórmulas:
donde:
x', y', z' = Coordenadas x,y,z transformadas
x, y, z = Coordenadas x,y,z originales
S = Escala
Tx, Ty, Tz = Traslaciones en x,y,z
m11...m33 = Coeficientes de la matriz de rotación
2D + 1D : Transformaciones de 3 dimensiones que utilizan Helmert 2D para planimetría y, traslación en z o traslación en z y pendientes x e y para altimetría.
Helmert 2D + Desplazamiento Vertical
Este tipo de transformación es una combinación de la transformación de 4 parámetros de Helmert y un desplazamiento en z. Esta traslación es la media de las diferencias de esta componente entre los puntos origen y destino.
Fórmulas:
donde:
x', y' = Coordenadas x,y transformadas
x,y = Coordenadas x,y originales
S = Escala
 = Ángulo de rotación
= Ángulo de rotaciónTx = Traslación x
Ty = Traslación y
Tz = Traslación z
Helmert 2D + Desplazamiento Vertical y Pendientes
Al igual que la transformación anterior, se trata de una combinación de la transformación de 4 parámetros de Helmert y una traslación en z calculada a partir de un desplazamiento e inclinaciones de la componentes x e y. Son necesarios al menos dos pares de puntos con coordenadas x e y, y tres con componente z.
Fórmulas:
donde:
x', y' = Coordenadas x,y transformadas
x,y = Coordenadas x,y originales
S = Escala
 = Ángulo de rotación
= Ángulo de rotaciónTx = Traslación x
Ty = Traslación y
Tz = Traslación z
Px = Pendiente x
Py = Pendiente y
X0 = Coordenada x original del primer par de puntos
Y0 = Coordenada y original del primer par de puntos
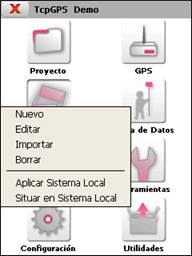
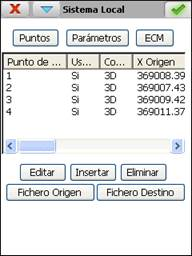
Para la gestión de los sistemas locales se presenta el siguiente menú de opciones:
Se distinguen dos modos para definir las transformaciones:
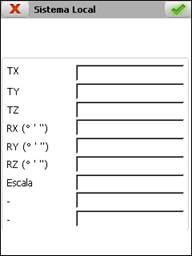
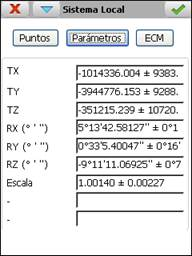
Por Parámetros : Introduciendo directamente los valores de los parámetros de las ecuaciones de transformación. Los desplazamientos se deben introducir en metros y el formato de los ángulos debe sexagesimal, en grados, minutos y segundos (separados por espacio), y sentido anti-horario con 0 en el Este.
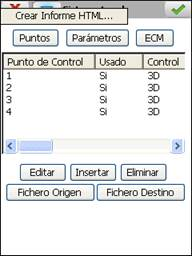
Por Puntos : Introduciendo una serie de pares de coordenadas origen y destino, 2D ó 3D, y calculando el sistema de ecuaciones del método seleccionado.
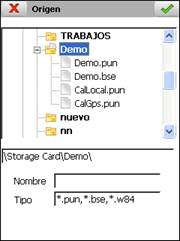
Se permite introducir los pares de puntos desde fichero, a través de los botones Fichero Origen y Fichero Destino, o de forma manual, pulsando el botón Insertar.
Los ficheros deben ser de tipo punto (*.PUN) o base (*.BSE). Para los datos origen también se admiten los ficheros de coordenadas geográficas con extensión *.W84, creados en la opción Gestión de Ficheros > Datos GPS.
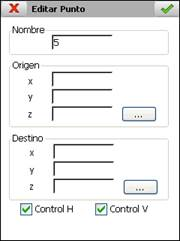
Si se introduce un punto manualmente se debe indicar el Nombre, las coordenadas Origen y Destino y si se utilizará para planimetría, Control H, altimetría, Control V, o en ambos casos. También es posible editar los valores de estos parámetros para cualquier punto sea cual sea el método de inserción.
El programa intenta resolver el sistema de ecuaciones de la transformación seleccionada cada vez que se realiza algún cambio en el listado de pares de puntos, ya sea insertando, editando o eliminando pares. Si se encuentra una solución, se mostrarán los valores calculados así como la desviación estándar de cada parámetro. El formato de los ángulos es sexagesimal, en grados, minutos y segundos, y sentido anti-horario con 0 en el Este. Los desplazamientos se muestran en metros.
Por otro lado, si se pulsa el botón ECM, se accede a la pantalla que muestra el error cuadrático medio y los residuos máximos de cada componente x, y, z. Dependiendo de la dimensión de la transformación, se calculan los siguientes errores cuadráticos:
2D : Error cuadrático medio H (x, y).
3D : Error cuadrático medio 3D (x,y,z), H (x, y), V(z).
2D + 1D : Error cuadrático medio H (x, y), V(z).
También se ofrece la posibilidad de crear un informe del sistema local a través de la opción Crear Informe HTML del menú de contexto.
Un ejemplo de éste se muestra a continuación:
Datos de Transformación
|
Fichero
|
D:\Transformaciones\Doc\InformeH2D.htm
|
|
Tipo
|
Helmert (transformación de semejanza de 4 parámetros) (2D)
|
|
Fecha y Hora
|
07/04/2011 13:27:33
|
Parámetros
|
TX
|
1050003.715 ± 0.123
|
|
TY
|
50542.131 ± 0.123
|
|
Rotación
|
176°46'54.97952'' ± 0°1'58.89222''
|
|
Escala
|
4.51962 ± 0.00058
|
Estadísticos
|
ECM
|
0.1142
|
|
Desviación Estándar
|
0.140
|
|
Residuo X Max
|
0.105 (Punto de Control 3)
|
|
Residuo Y Max
|
0.106 (Punto de Control 3)
|
Puntos de Control
|
Número de Puntos de Control
|
3
|
|
Punto de Control
|
Usado
|
X Origen
|
Y Origen
|
Z Origen
|
X Destino
|
Y Destino
|
Z Destino
|
Residuo X
|
Residuo Y
|
|
1
|
Si
|
121.622
|
-128.066
|
50.000
|
1049422.400
|
51089.200
|
30.000
|
0.004
|
-0.029
|
|
2
|
Si
|
141.228
|
187.718
|
40.000
|
1049413.950
|
49659.300
|
20.000
|
0.101
|
-0.077
|
|
3
|
Si
|
175.802
|
135.728
|
30.000
|
1049244.950
|
49884.950
|
10.000
|
-0.105
|
0.106
|
Una vez calculados o introducidos manualmente los parámetros se debe pulsar el botón aceptar para crear el sistema local. Se trata de un fichero ASCII con extensión NTR y con el siguiente formato (ejemplo de transformación Helmert 2D):
[Type]
2D Helmert (4-parameter similarity transformation)
[Parameters]
1050003.71454
50542.13112
3.085426889
4.519620520
[Inverse Parameters]
232582.62262
-1876.44668
-3.085426889
0.221257507
[MSE]
3D 0.0000 H 0.1142 V 0.0000
[Inverse MSE]
3D 0.0000 H 0.0253 V 0.0000
[Standard Deviation]
0.140
[Max X Residual]
0.105 (Control Point 3)
[Max Y Residual]
0.106 (Control Point 3)
[Control Points]
3
[Point Used HControl VControl XSource YSource ZSource XTarget YTarget ZTarget XRes YRes ZRes]
1 1 1 1 121.622 -128.066 50.000 1049422.400 51089.200 30.000 0.004 -0.029 ?
2 1 1 1 141.228 187.718 40.000 1049413.950 49659.300 20.000 0.101 -0.077 ?
3 1 1 1 175.802 135.728 30.000 1049244.950 49884.950 10.000 -0.105 0.106 ?
Después de crear el fichero de transformación será necesario ir a la opción Proyecto > Propiedades y seleccionarlo en el listado Sistema Local. Si se ha grabado en un directorio distinto al del proyecto actual, se debe copiar a éste utilizando la opción Sistema Local > Importar. Esta opción ofrece la posibilidad de activarlo directamente sin tener que hacerlo en propiedades de proyecto.